Esta análise d’Os Elementos foi extraída do livro History of Greek Mathematics – vol. 1.
Livro I
O Livro I d’Os Elementos começa necessariamente com a matéria preliminar essencial, classificada sob os títulos de Definições (ὅροι), Postulados (αἰτήματα) e Noções Comuns (κοιναὶ ἔννοιαι). Ao chamar os axiomas de Noções Comuns, Euclides seguiu o exemplo de Aristóteles, que usa como alternativas para “axiomas” os termos “comuns (coisas)”, “opiniões comuns”.
Muitas das Definições estão abertas a críticas de uma maneira ou de outra. Duas delas, pelo menos, parecem ser originais, a saber, as definições de uma linha reta (4) e de uma superfície plana (7); por mais insatisfatórias que sejam, parecem ser capazes de uma explicação simples. A definição de uma linha reta é aparentemente uma tentativa de expressar, sem qualquer apelo à visão, o sentido da definição de Platão “aquilo do qual o meio encobre as extremidades” (a saber. para um olho colocado em uma extremidade e olhando ao longo dela); e a definição de uma superfície plana é uma adaptação da mesma definição. Mas a maioria das definições provavelmente foram extraídas de livros-texto anteriores; algumas parecem ser inseridas apenas por respeito à tradição, por exemplo, as definições de oblongo, losango, rombóide, que nunca são consideradas n’Os Elementos. As definições de diversas figuras supõem a existência da coisa definida, por exemplo, o quadrado, e os diferentes tipos de triângulo sob sua dupla classificação, (a) com referência a seus lados (equilátero, isósceles e escaleno) e (b) com referência a seus ângulos (em ângulo reto, em ângulo obtuso e em ângulo agudo); tais definições são provisórias enquanto se aguarda a comprovação da existência por meio da construção real. Um paralelogramo não é definido; sua existência é provada primeiramente em I. 33, e na proposição seguinte é chamada de “área de paralelogramo”, que significa uma área contida por linhas paralelas, em preparação para o uso da simples palavra “paralelogramo” de I. 35 em diante. A definição do diâmetro de um círculo (17) inclui um teorema; pois Euclides acrescenta que “tal linha reta também divide o círculo”, que é um dos teoremas atribuídos a Thales; mas tal adição era realmente necessária em vista da próxima definição (18), pois, sem essa explicação, Euclides não se justificaria ao descrever um semicírculo como uma porção de um círculo cortado por um diâmetro.
De longe, os cinco postulados são especialmente importantes, pois é neles que Euclides estabelece os verdadeiros princípios da geometria euclidiana; e nada mostra mais claramente sua determinação em reduzir ao mínimo suas suposições originais. Os três primeiros postulados são comumente considerados como os postulados da construção, pois eles afirmam a possibilidade (1) de traçar a linha reta unindo dois pontos, (2) de produzir uma linha reta em qualquer direção, e (3) de descrever um círculo com um determinado centro e ‘distância’. Todavia eles implicam muito mais do que isso. Nos postulados 1 e 3 Euclides postula a existência de linhas retas e círculos, e responde implicitamente às objeções daqueles que poderiam dizer que, de fato, as linhas retas e círculos que podemos desenhar não são linhas retas e círculos matemáticos; Euclides pode supostamente afirmar que podemos, no entanto, assumir nossas linhas retas e círculos como tais para o propósito de nossas provas, uma vez que elas são apenas ilustrações que nos permitem imaginar as coisas reais que elas representam imperfeitamente. Ademais. os Postulados 1 e 2 implicam ainda que a linha reta traçada no primeiro caso e a parte produzida da linha reta no segundo caso são únicas; em outras palavras, o postulado 1 implica que duas linhas retas não podem delimitar um espaço, e assim torna desnecessário o ‘axioma’ para esse efeito interpolado na Proposição 4, enquanto o postulado 2 implica de forma semelhante o teorema de que duas linhas retas não podem ter um segmento comum, o que Simson sugeriu como corolário à I.11.
À primeira vista, os Postulados 4 (que todos os ângulos retos são iguais) e 5 (o Postulado das paralelas) podem parecer ser de um caráter totalmente diferente, já que são mais da natureza de teoremas não comprovados. No entanto, o Postulado 5 é facilmente visto como ligado a construções, uma vez que muitas construções dependem da existência e do uso de pontos nos quais as linhas retas se interceptam; é, portanto, absolutamente necessário estabelecer algum critério pelo qual possamos julgar se duas linhas retas em uma figura irão ou não encontrar-se, se forem produzidas. O postulado 5 serve a esse propósito, assim como ao de fornecer uma base para a teoria das linhas paralelas. A rigor, Euclides deveria ter ido mais longe e ter dado critérios para se julgar se outros pares de linhas — por exemplo, uma linha reta e um círculo, ou dois círculos — em uma determinada figura irão ou não se cruzar. Mas isso teria exigido uma série considerável de proposições, que teria sido difícil de formular em um estágio tão precoce, e Euclides preferiu assumir provisoriamente tais interseções em certos casos, por exemplo, em I.1.
O postulado 4 é frequentemente classificado como um teorema. Porém, de qualquer maneira, era necessário colocá-lo antes do Postulado 5 pela simples razão de que o Postulado 5 não apresentaria critério de maneira alguma, a menos que os ângulos retos fossem magnitudes determinadas; o Postulado 4 os declara então como tal. No entanto, isso não é tudo. Se o postulado 4 fosse provado como um teorema, ele só poderia ser provado mediante a aplicação de um par de ângulos retos ‘adjacentes’ a outro par. Tal método não seria válido a menos que se assumisse a invariabilidade das figuras, que, portanto, teria que ser afirmada como um postulado antecedente. Euclides preferiu afirmar como um postulado, diretamente, o fato de que todos os ângulos retos são iguais; portanto, seu postulado pode ser considerado como equivalente ao princípio da invariabilidade das figuras, ou, o que é a mesma coisa, a homogeneidade do espaço.
Pelas razões que dei acima1, penso que o grande postulado 5 pertence ao próprio Euclides; e parece provável que o postulado 4 seja também seu, se não também os postulados 1-3.
Sobre as Noções Comuns, há boas razões para acreditar que apenas cinco (no máximo) são genuínas, as três primeiras e duas outras, a saber ‘Coisas que coincidem quando aplicadas uma à outra são iguais umas às outras’ (4), e ‘O todo é maior que as partes’ (5). A objeção a (4) é que ela é incontestavelmente geométrica e, portanto, segundo os princípios de Aristóteles, não deve ser classificada como um “axioma”; é uma definição mais ou menos suficiente de igualdade geométrica, mas não um axioma real. Euclides evidentemente não gostou do método de sobreposição para provar a igualdade, sem dúvida porque ele assume a possibilidade de movimento sem deformação. Porém, ele não poderia prescindir totalmente dela. Assim, em I.4 ele praticamente teve que escolher entre usar o método e assumir toda a proposição como um postulado. Todavia, ele não cita a Noção Comum 4; ele diz ‘a base BG coincidirá com a base EF e será igual a ela’. Da mesma forma, em I. 6 ele não cita a Noção Comum 5, mas diz ‘o triângulo DEC será igual ao triângulo AGB, o menor é o maior, o que é um absurdo’. Parece provável, portanto, que mesmo essas duas Noções Comuns, embora aparentemente reconhecidas por Proclus, foram generalizações de inferências particulares encontradas em Euclides e foram inseridas após seu tempo.
As Proposições do Livro I se dividem em três grupos distintos. O primeiro grupo consiste nas Proposições 1-26, lidando principalmente com triângulos (sem o uso de paralelas), mas também com perpendiculares (11, 12), duas linhas retas entrecruzadas (15), e uma linha reta em pé sobre outra, mas não cortando-a, e formando ângulos ‘adjacentes’ ou suplementares (13, 14). A Proposição 1 dá como base a construção de um triângulo equilátero sobre uma linha reta dada; isso é colocado aqui não tanto por sua própria conta, mas porque é imediatamente necessário para construções (em 2, 9, 10, 11). A construção em 2 é uma continuação direta das construções mínimas assumidas nos Postulados 1-3, e nos permite (já que os Postulados não o fazem) transferir um determinado comprimento de linha reta de um lugar para outro; em 3, isso leva à operação tão frequentemente exigida de se cortar de uma linha reta dada um comprimento igual a outro. 9 e 10 são os problemas de bissecionar um determinado ângulo e uma determinada linha reta respectivamente, e 11 mostra como erguer uma perpendicular a uma determinada linha reta a partir de um determinado ponto sobre ela. A construção como meio de se provar a existência está em evidência no Livro, não apenas em 1 (o triângulo equilátero), mas em 11, 12 (perpendiculares erguidas e postas), e em 22 (construção de um triângulo no caso geral onde os comprimentos dos lados são dados); 23 constrói, por meio de 22, um ângulo igual a um determinado ângulo retilíneo. As proposições sobre triângulos incluem os teoremas de congruência (4, 8, 26) — omitindo o “caso ambíguo” que só é levado em conta na proposição análoga (7) do Livro VI — e os teoremas (aliados a 4) sobre dois triângulos em que dois lados de um são respectivamente iguais a dois lados do outro, mas em relação aos ângulos incluídos (24), ou às bases (25), um é maior que o outro, e está provado que o triângulo em que o ângulo incluído é maior tem a base maior e vice-versa. A Proposição 7, usada para provar a Proposição 8, também é importante como sendo o equivalente do Livro I ao do Livro III.10 (que dois círculos não podem se cruzar em mais pontos do que dois). Depois temos os teoremas sobre triângulos simples em 5, 6 (os triângulos isósceles têm os ângulos opostos aos lados iguais — o teorema de Thales e o inverso), a importante proposição 16 (o ângulo exterior de um triângulo é maior que qualquer um dos ângulos interiores e opostos) e sua derivada 17 (quaisquer dois ângulos de um triângulo são, juntos, menores que dois ângulos retos), 18, 19 ( o ângulo maior subtendido por um lado maior e vice-versa), 20 (quaisquer dois lados juntos, são maiores que o terceiro). Este último fornece o διορισμός necessário, ou o critério de possibilidade, do problema em 22, de construir um triângulo a partir de três linhas retas de determinado comprimento, o qual, portanto, teve que vir depois e não antes de 20. 21 (provando que os dois lados de um triângulo que não seja a base são, juntos, maiores, mas incluem um ângulo menor, do que os dois lados de qualquer outro triângulo na mesma base, mas com vértice dentro do triângulo original) é útil para a prova da proposição (não declarada em Euclides) segundo a qual, de todas as linhas retas traçadas a partir de um ponto externo a uma dada linha reta, a perpendicular é a mais curta, e a mais próxima da perpendicular é menor do que a mais remota.
O segundo grupo (27-32) inclui a teoria das paralelas (27-31, terminando com a construção através de um dado ponto de uma paralela a uma dada linha reta); e então, em 32, Euclides prova que a soma dos três ângulos de um triângulo é igual a dois ângulos retos por meio de uma paralela a um lado, traçada a partir do vértice oposto (cf. a prova Pitagórica, ligeiramente diferente, pg. 143 [deste livro]).
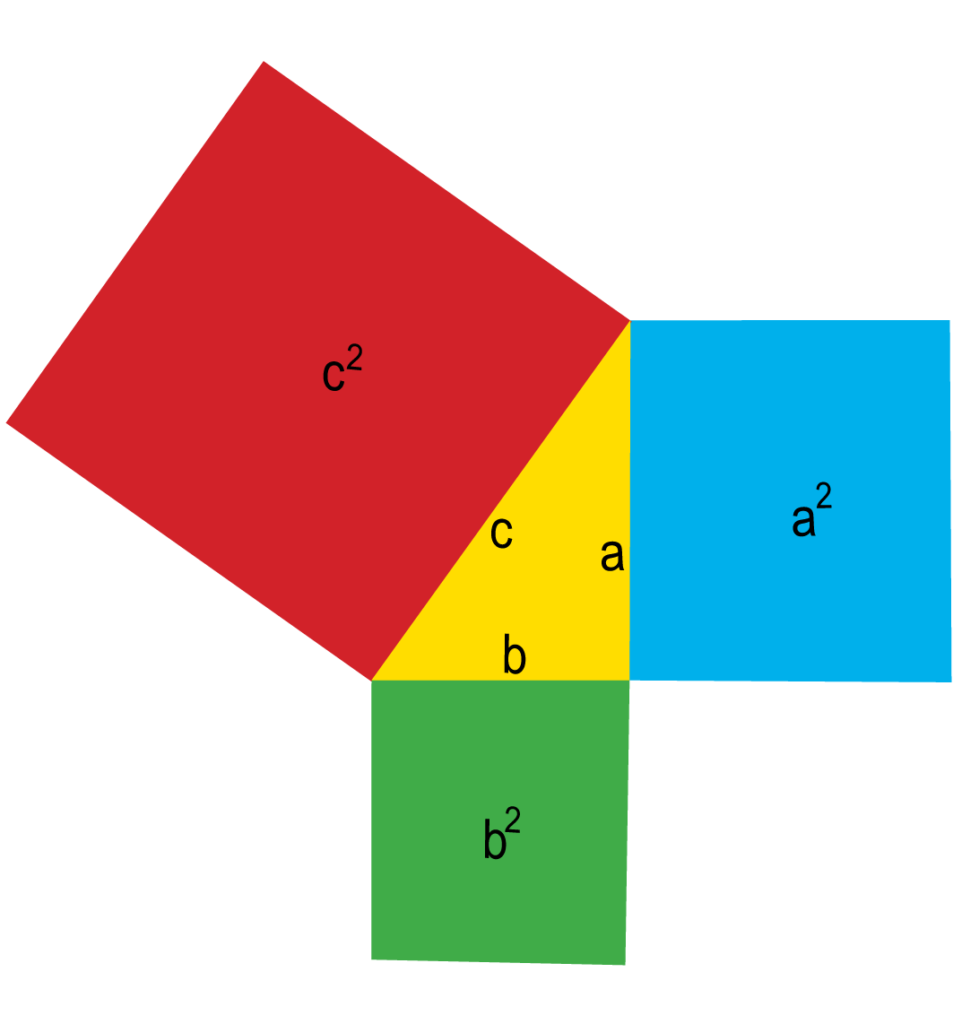
O terceiro grupo de proposições (33-48) trata geralmente de paralelogramos, triângulos e quadrados com referência a suas áreas. 33, 34 são a prova da existência e da propriedade de um paralelogramo, e então somos introduzidos a uma nova concepção, a de figuras equivalentes, ou figuras iguais em área, embora não iguais no sentido de congruente: paralelogramos na mesma base ou em bases iguais e entre as mesmas paralelas são iguais em área (35, 36); o mesmo se aplica aos triângulos (37, 38), e um paralelogramo na mesma base (ou igual) com um triângulo e entre as mesmas paralelas é o dobro do triângulo (41). 39 e o 40 interpolado são conversões parciais de 37 e 38. O teorema 41 nos permite ‘construir, em um determinado ângulo retilíneo, um paralelogramo igual a um determinado triângulo’ (42). As proposições 44, 45 são da maior importância, sendo os primeiros casos do método pitagórico de “aplicação de áreas”, “aplicar a uma dada linha reta, em um dado ângulo retilíneo, um paralelogramo igual a um dado triângulo (ou figura retilínea)”. A construção em 44 é notavelmente engenhosa, sendo baseada na de 42 combinada com a proposição (43) que prova que os ‘complementos dos paralelogramas sobre o diâmetro’ em qualquer paralelogramo são iguais. Assim, somos capazes de transformar um paralelogramo de qualquer forma em outro com o mesmo ângulo e de igual área, mas com um lado de qualquer comprimento, digamos, um comprimento unitário; isso é o equivalente geométrico da operação algébrica de dividir o produto de duas quantidades por um terceiro. A proposição 46 constrói um quadrado sobre uma determinada linha reta como lado, e é seguida pelo grande teorema de Pitágoras acerca do quadrado da hipotenusa de um triângulo em ângulo reto (47) e seu inverso (48). A prova notavelmente inteligente de 47 por meio da conhecida figura do “moinho de vento” e a aplicação a ela de I. 41 combinado com I. 4 parece ser de responsabilidade do próprio Euclides; é realmente equivalente a uma prova pelos métodos do Livro VI (Proposições 8, 17), e a realização de Euclides foi a de evitar o uso de proporções e tornar a prova dependente apenas do Livro I.
Não peço desculpas por ter lidado longamente com o Livro I e, em particular, com o assunto preliminar, em vista da posição única e da autoridade dos Elementos como uma exposição dos princípios fundamentais da geometria grega, e a necessidade para o historiador da matemática de uma compreensão clara de sua natureza e plena importância. Agora será possível lidar mais sumariamente com os outros Livros.
Notas:
[1] páginas. 339, 358 do livro.
Se esta tradução foi útil para você, apoie nosso projeto através de um Pix de qualquer valor para que possamos continuar trazendo mais conteúdos como esse. Agradecemos imensamente pelo seu apoio! Chave Pix: diariointelectualcontato@gmail.com